task.py
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Cipher import AES
import hashlib
import os
import base64
from gmpy2 import is_prime
FLAG = open("flag").read()
FLAG += (16 - (len(FLAG) % 16))*" "
class Rng:
def __init__(self, seed):
self.seed = seed
self.generated = b""
self.num = 0
def more_bytes(self):
self.generated += hashlib.sha256(self.seed).digest()
self.seed = long_to_bytes(bytes_to_long(self.seed) + 1, 32)
self.num += 256
def getbits(self, num=64):
while (self.num < num):
self.more_bytes()
x = bytes_to_long(self.generated)
self.num -= num
self.generated = b""
if self.num > 0:
self.generated = long_to_bytes(x >> num, self.num // 8)
return x & ((1 << num) - 1)
class DiffieHellman:
def gen_prime(self):
prime = self.rng.getbits(512)
iter = 0
while not is_prime(prime):
iter += 1
prime = self.rng.getbits(512)
print("Generated after", iter, "iterations")
return prime
def __init__(self, seed, prime=None):
self.rng = Rng(seed)
if prime is None:
prime = self.gen_prime()
self.prime = prime
self.my_secret = self.rng.getbits()
self.my_number = pow(5, self.my_secret, prime)
self.shared = 1337
def set_other(self, x):
self.shared ^= pow(x, self.my_secret, self.prime)
def pad32(x):
return (b"\x00"*32+x)[-32:]
def xor32(a, b):
return bytes(x^y for x, y in zip(pad32(a), pad32(b)))
def bit_flip(x):
print("bit-flip str:")
flip_str = base64.b64decode(input().strip())
return xor32(flip_str, x)
alice_seed = os.urandom(16)
while 1:
alice = DiffieHellman(bit_flip(alice_seed))
bob = DiffieHellman(os.urandom(16), alice.prime)
alice.set_other(bob.my_number)
print("bob number", bob.my_number)
bob.set_other(alice.my_number)
iv = os.urandom(16)
print(base64.b64encode(iv).decode())
cipher = AES.new(long_to_bytes(alice.shared, 16)[:16], AES.MODE_CBC, IV=iv)
enc_flag = cipher.encrypt(FLAG)
print(base64.b64encode(enc_flag).decode())
코드 해석

이 부분을 통해서 alice와 bob은 Diffie Hellman 키 교환을 여러 번 반복한 것을 알 수 있다.
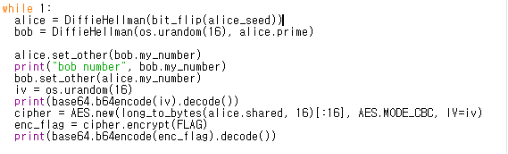
DiffieHellman에 bit_flip(alice_seed)라는 값을 매개 값으로 넘겨주므로 bit_flip()함수를 먼저 보았다.
먼저 alice_seed는 alice_seed=os.urandom(16) 을 통해서 16바이트 크기의 unsigned 값을 만들어준다는 것을 알 수 있다.

bit_flip은 16이라는 값을 x로 받고, flip_str이라는 변수에 입력받은 값의 양쪽 모든 공백을 삭제하고 base64로 디코딩을 한 값을 넣게 된다. 그리고 xor32 함수에 flip_str와 x값인 16을 넘겨준다.

xor32함수는 a로 flip_str, b로 x값을 받는다. 그리고 for문을 통해서 bytes안에 있는 값들을 바이트 객체로 만들어준다. bytes는 1바이트 단위의 값을 연속적으로 저장하는 시퀀스 자료형이다. bytes안에서 for문을 통해 반복문을 실행한다. 여기서 zip()은 동일한 개수로 이루어진 pad32(a), pad32(b)를 묶어주는 역할을 하는 내장함수이다. pad32()는 함수인데, 매개값으로 받은 a, b를 각각 (b”\x00”*32+a)[-32:], (b”\x00”*32+b)해준 다음 return해준다.
return된 값을 받은 bit_flip()은 DiffieHellman 클래스로 가게 된다.
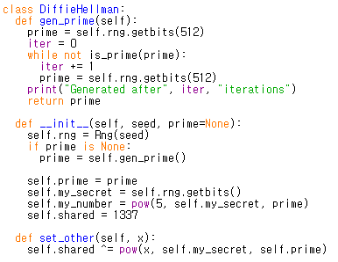
DiffieHellman의 __init__()을 보면 self.my_secret = self.rng.getbits()가 있다.
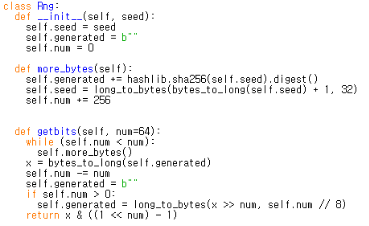
Rng클래스의 getbits()부분을 보았다. self.num이 num보다 작으면 위에 있는 more_bytes()로 가게 된다. more_bytes()에서는 해시함수 라이브러리를 사용해서 SHA256암호화를 해준다음, digest()을 통해 16진수 형식으로 반환하며 ASCII로 변환 가능한 것들을 특수문자나 숫자 등으로 변환해서 보여준다. 그리고 self.seed에 long_to_bytes를 통해 long int형을 byte string으로 변환해준다. 그리고나서 self.num을 +256해준다.
다시 getbits()로 돌아와 self.num이 num보다 크면 x에 more_bytes에서 생성했던 byte string형이었던 self_generated를 long int형으로 다시 바꿔준다. 그리고 나서 self.num을 num만큼 감소시킨다. self.generated값을 b””을 통해 다시 byte string형으로 바꿔준다. x를 오른쪽으로 num번 이동해준 값과 self.num을 8로 나눈 몫값을 long_to_bytes해준다. 그리고 x와 1을 num번 왼쪽으로 이동한 값에서 1을 빼준 값을 return 해준다.
다시 DiffieHellman 클래스로 돌아가보았다. __init__()에서 prime = self.gen_prime()이기 때문에 gen_prime()으로 가 보았다. 보니까 prime을 Rng클래스의 getbits에 num을 256으로 지정해서 getbits()을 실행해서 return받는다. 그 prime값을 __init__에서 self.prime에 넣어주고 num이 64으로 지정된 getbits()을 실행한 값을 self.my_secret에 넣어준다. self.my_number에는 pow()함수를 통해 제곱한 결과를 넣어준다. set_other()함수에서는 1337로 지정해뒀던 self.shard에 pow함수를 통해서 구한 제곱 결과를 self.shard값과 XOR해서 넣어준다.
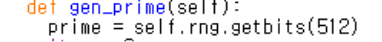
이 부분에서 getbits함수에 512를 self.num으로 전송이 될 때

이 부분이 실행되지 않는다. 이에 따라 self.generated가 다음 호출을 위해서 초기화가 되고, 이것은 코드의 결함이다. seed의 값과 prime의 값을 수동으로 테스트한 결과 끝에서 두 번째 비트를 뒤집었을 때 반복 횟수가 감소하면 0이 되고 그렇지 않으면 1이 된다. 결국 마지막 바이트에 대해서 0또는 1로 무차별 대입을 해야 한다. 마지막 바이트가 미정인 상태로 우리가 생각해야 할 비트 개수만큼 찾을 수 있는 스크립트를 작성해야 한다.
공격 스크립트 (flflag.py)
from pwn import *
from base64 import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
import subprocess
from task import Rng , DiffieHellman
def POW(r):
print("----------Solving POW-----------")
command = r.recv().strip().split(b": ")[-1]
hashed = subprocess.check_output(command,shell=True).strip()
r.sendline(hashed)
print("----------Solved----------------")
def sendloop(r,i: int):
r.recv()
a = b64encode(long_to_bytes(i,32))
r.sendline(a)
iters = int(r.recvline().strip().split(b" ")[2])
bob_number = int(r.recvline().strip().split(b" ")[-1]) # bob number
iv = b64decode(r.recvline().strip()) # IV
ciphertext = b64decode(r.recvline().strip()) # ciphertext
return iters,bob_number,iv,ciphertext
def get_flag(seed,bob_number,iv,ciphertext):
alice = DiffieHellman(long_to_bytes(int(seed,2)))
shared = pow(bob_number,alice.my_secret,alice.prime)
cipher = AES.new(long_to_bytes(shared,16)[:16] , AES.MODE_CBC , IV= iv)
flag = cipher.decrypt(ciphertext)
return flag
r = remote("bitflip1.hackable.software",1337)
POW(r)
bits = ""
for pos in range(1,128):
nums = 0 if bits=='' else int(bits,2)*2
flippedbit = 1<<pos | ((nums//2)^((1<<(pos-1))-1))*2
iters1, iters2 = sendloop(r,nums)[0], sendloop(r,flippedbit)[0]
assert iters2 != 0 # to check they generate the same prime, if not rerun script
bits = "1" + bits if iters1 +1 == iters2 else "0" + bits
iters,bob_number,iv,ciphertext = sendloop(r,0)
#guessing LSB
flag = get_flag(bits+"0",bob_number,iv,ciphertext)
print(flag)
flag = get_flag(bits+"1",bob_number,iv,ciphertext)
print(flag)
r.close()
스크립트 실행 시 flag 값을 얻을 수 있다


'[CTF] Dragon CTF 2020' 카테고리의 다른 글
| RetroZeit(Reverse) (0) | 2023.12.21 |
|---|---|
| Harmony Chat(Webhacking) (0) | 2023.12.21 |
| Bit Flip3(Cryptography) (1) | 2023.12.21 |
| Bit Flip2(Cryptography) (1) | 2023.12.21 |